Measuring Price Elasticity of Demand- Proportionate or Percentage Method

 

 Learning Contents:                                                            

·         Introduction to Proportionate method of Price Elasticity of Demand

·         Questions For Practice

 

Proportionate or Percentage Method

It is one of the commonly used method for measuring the price elasticity of demand. In this method, the elasticity of demand is calculated as the percentage change in quantity demanded divided by the percentage change in price. The formula for calculating the elasticity of demand is given below:
















Interpreting Elasticity of Demand using Percentage Elasticity of Demand 

Case

Description

Degree of elasticity

Numerically, Ed

1.

If the calculated value is more than 1

 

More than Unitary Elastic or Elastic Demand

 

Ed>1

2.

If the calculated value is equal to 1

Unitary Elastic Demand

 

Ed=1

3.

If the calculated value is less  than 1

Less than Unitary Elastic Demand or Inelastic Demand

 

Ed<1


Questions for Practice:

1. When the price of a commodity was ₹10 per unit, its demand in the market was 50 units per day. When the price of the commodity fell to ₹ 8, the demand rose to 60 units. Here, the price elasticity of demand can be calculated as

Solution:

Following information is given:

 

Q = 50 units

 

Q1= 60 units

 ΔQ =Q1-Q

      =60-50

      =10

 

P = ₹ 10

 

P1= ₹8

ΔP = P1-P

     =8-10

     = -2

       

                                     Ed=?












Note:  (-) negative sign is prefixed to the formula because price and demand are inversely related. Doing this would bring the value of elasticity of demand to positive. 

Interpretation:

The calculated value of Elasticity of demand(Ed) is 1 indicates unitary elastic demand. It implies that a 1% fall in the price of the commodity caused a 1% increase in its demand showing that change in demand is equal to change in price.

2. The quantity of a good demanded rises from 1 unit to 4 units when the price falls from ₹4 to ₹ 2 per unit. The price elasticity of demand for the good is approximately:

Solution:

Following information is given:

 

Q = 1 unit

 

Q1= 4 units

 ΔQ =Q1-Q

      =4-1

      =3

 

P = ₹ 4

 

P1= ₹2

ΔP = P1-P

     =2-4

     = -2

       

                                     Ed=?











Note:  (-) negative sign is prefixed to the formula because price and demand are inversely related. Doing this would bring the value of elasticity of demand to positive. 

Interpretation:

The above calculated value of Elasticity of demand(Ed) is 6 >1 indicates more than unitary elastic demand. It implies that a 1% fall in the price of good causes 6% increase in its demand showing that change in demand is greater than the change in price.

3. At ₹26 per unit, the demand for a commodity is 30 units. If the price increases from ₹26 to ₹30 per unit, the demand decreases to 15 units. Calculate the price elasticity of demand.

Solution:

Following information is given:

 

Q = 30 units

 

Q1= 15 units

 ΔQ =Q1-Q

      =15-30

      = -15

 

P = ₹ 26

 

P1= ₹30

ΔP = P1-P

     =30-26

     = 4

       

                                     Ed=?

 











Note:  (-) negative sign is prefixed to the formula because price and demand are inversely related. Doing this would bring the value of elasticity of demand to positive. 


Interpretation:

The above calculated value of Elasticity of demand(Ed) is 3.25 >1 indicates more than unitary elastic demand. It implies that a 1% rise in the price of the commodity causes 3.25% fall in its demand showing that change in demand is greater than change in price. 

4. When the price of a good falls from ₹10 to ₹8 per unit, its demand rises from 20 units to 24 units. What will be its price elasticity of demand?

Solution:

Following information is given:

 

Q = 20 units

 

Q1= 24 units

 ΔQ =Q1-Q

      =24-20

      = 4

 

P = ₹ 10

 

P1= ₹8

ΔP = P1-P

     =8-10

     = -2

       

                                     Ed=?




Note:  (-) negative sign is prefixed to the formula because price and demand are inversely related. Doing this would bring the value of elasticity of demand to positive. 


Interpretation:

The above calculated value of Elasticity of demand(Ed) is 1 indicates unitary elastic demand. It implies that a 1% fall in the price of good causes a 1% rise in its demand showing that change in demand is equal to change in price.

Thanks & please Share with your friends  

Comment if you have any questions.



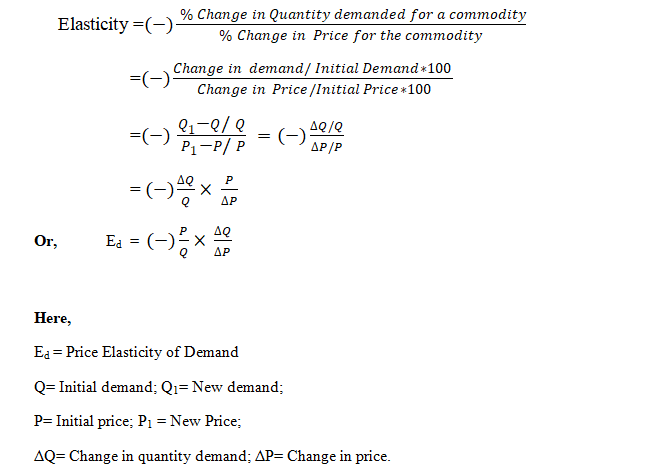
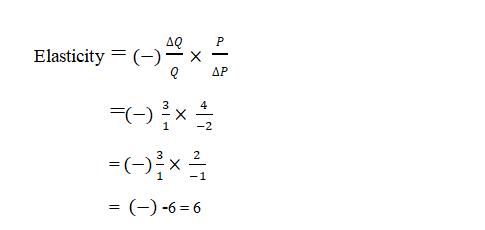
Comments

Post a Comment

Popular posts from this blog

SHIFTS & ROTATIONS IN PRODUCTION POSSIBILITY CURVE

Image
    Learning Contents:                                                                Shifts   in   PPC  Rotations in PPC Change in Production Possibility Curve (Shifting/Rotation) The change in the Production Possibility curve can be of two types:  Shift in PPC: PPC will shift when there is a change in productive capacity (resources or technology) with respect to both the goods. Rotation of PPC: PPC will rotate when there is a change in productive capacity (resources or technology) with respect to only one good. Shifts in PPC:   The shift in PPC can either be rightward or backward. These shifts bring about a change in the production of both goods in an economy. The shifts in PPC are of two types: Rightward shift in PPC: Rightward shift in PPC occurs when the resources are increased or technology is improved for the production of both goods that means we can produce more of both the goods. Accordingly, PPC shifts to the right from Initial PPC (AB) to Final PPC (CD).   Re
Read more »500

Income Elasticity: Luxury Goods, Necessity Goods, and Inferior Goods.

Image
  Learning Contents:                                                               ·         Understanding Income Elasticity with respect of luxury goods, necessity goods and inferior goods. The demand for a commodity not only depends on the price of a commodity but also the income level of the consumer. It is a general understanding that a consumer usually prefers to spend more when his income rises and less when his income falls. Sometimes, we might also experience a fall in the demand of certain goods and services even when income rises. Therefore, income elasticity varies with respect to different types of goods and services. The income elasticity measures the percentage change in quantity demanded as a result of percentage change in the income of the consumer. The formula of income elasticity of demand is, The income elasticity measures the demand’s sensitivity or responsiveness to the change in income.   In simple words, it measures to what extent demand changes as a result o
Read more »500

CONSUMER’S PREFERENCES AND INDIFFERENCE MAP

Image
    Learning Contents:                                                               ·          Understanding Consumer preferences and Indifference curve. ·          Understanding Indifference Map. Introduction: The concept of the indifference map is based upon the concept of consumer preferences. So, it is important to first understand the concept of consumer preferences. Consumer’s Preferences: Preferences indicate individual tastes, likings, etc. that determine the amount of pleasure, happiness people get from the consumption of the goods and services and measured by the utility of various bundles or combinations of goods. It allows the consumers to rank these bundles of goods according to the levels of utility it provides them. Note that preferences are independent of income and prices. The ability to purchase goods does not determine a consumer’s likes or dislikes. One can have a preference for Rolex watches over Titan but only have the financial means to wear a titan
Read more »500